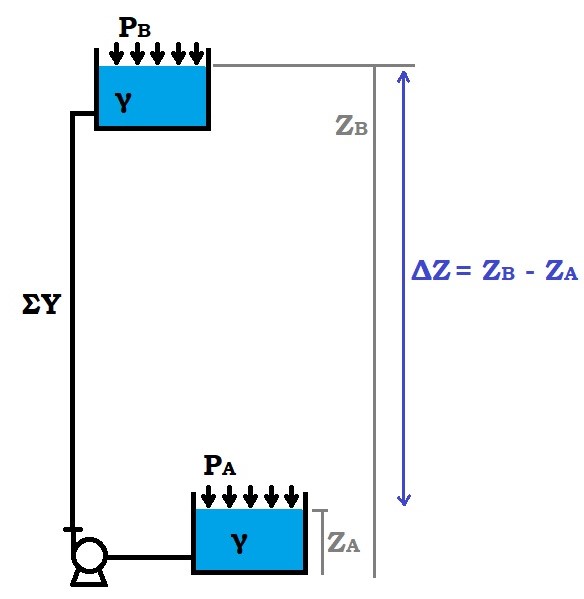
Each centrifugal pump is associated with its own characteristic curve, which is the graphical representation of the pump's performance.
- On the x-axis (horizontal axis), the flow rate Q is indicated, usually in m3/h. It represents the amount of fluid passing through each section of the centrifugal pump over a defined period. This quantity depends on the dimensional characteristics of the pump, the number of motor revolutions (thus the rotational speed of the impeller), and the characteristics of the fluid (density and viscosity depending on temperature). The flow rate influences all the performances of the centrifugal pump and is the first technical parameter to consider.
- On the y-axis (vertical axis), the head H is indicated, usually in meters. It is calculated from the pressure difference between the outlet and the inlet of the centrifugal pump and represents how far the fluid can be pushed if it encounters resistance in its path like height, curves, or valves.